9.2. Уравнения состояния и закономерности движения газа
9. ПНЕВМАТИЧЕСКИЕ СИСТЕМЫ
9.2. Уравнения состояния и закономерности движения газа
Газы, у которых отсутствуют силы сцепления между молекулами, а сами молекулы представляют собою материальные точки, не имеющие объема, называются идеальными. В природе идеальных газов не существует, и в термодинамику их вводят условно для получения более простых расчетных формул, определяющих свойства рабочих тел. Однако не все известные в природе газы можно, даже условно, считать идеальными. Водяной пар и пары некоторых других веществ можно отнести к идеальным газам только при их определенном состоянии.
Возможность рассмотрения известных в природе газов как идеальных зависит от того, насколько состояние данного газа близко к состоянию перехода в жидкость, т.е. к состоянию сжижения или насыщения. Известно, что любой газ при определенных условиях можно перевести в жидкое состояние; чем ниже температура и выше давление, тем ближе состояние данного газа к состоянию насыщения. При этом силы сцепления между молекулами возрастают, и объем молекул становится соизмеримым с объемом межмолекулярного пространства. В этом случае данные газы существенно отличаются от свойств идеальных газов и их свойства надо определять по другим уравнениям.
Водяной пар, например, входящий в газовые смеси, образующиеся при сгорании топлива в топках паровых котлов или в цилиндрах тепловых двигателей, можно отнести к идеальному газу. Водяной пар, используемый как рабочее тело в паровых двигателях или в теплообменных аппаратах. К идеальному газу отнести нельзя, так как здесь уже нельзя пренебрегать силами сцепления между молекулами и объемом самих молекул.
В результате изучения свойств идеальных газов установлено, что для любого газа произведение абсолютного давления на удельный объем, деленное на абсолютную температуру газа, есть величина постоянная, т.е.

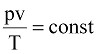 , (9.1)
, (9.1)
где р – абсолютное давление газа;
v – удельный объем газа, v = V/M = 1/r, здесь V – объем, занимаемый газом, M – масса газа, r – плотность газа;
Т – абсолютная температура (°К).
Постоянная величина в данном уравнении обозначается буквой R и называется удельной газовой постоянной. Поэтому уравнение можно записать в другом виде:
 ,
,
или (9.2)
 ,
,
где R – удельная газовая постоянная, Дж/(кг·град).
Для каждого идеального газа определяется своя удельная газовая постоянная. Для воздуха удельная газовая постоянная R = 287 Дж/(кг·град).
Уравнение (9.2) называется уравнением состояния идеального газа, или его характеристическим уравнением, и используется при термодинамических расчетах свойств идеальных газов.
Чтобы использовать уравнение (9.2) для любого количества газа, его преобразуют, выразив удельный объем v через массу M и объем V , т.е.:
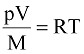 ,
,
или (9.3)
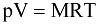 .
.
Из уравнения состояния идеального газа выводятся уравнения состояния газа при различных термодинамических процессах:
- для изотермического процесса pv = const;
- для изобарического процесса v/T = const;
- для изохорного процесса p/T= const.
В термодинамике введено понятие о килограмм-молекуле газа (киломоле), под которым подразумевается масса газа в килограммах, численно равная молекулярной массе газа. Киломоль, как и молекулярная масса, обозначается буквой m и имеет размерность [кг/моль].
Установлено , что при нормальных физических условиях, т.е. при p = 1,013×105 Н/м2 и t = 0°С, один киломоль любого газа занимает объем 22,4 м3/кмоль, т.е. mv = 22,4 м3/кмоль .
В других условиях эта величина будет иной, но одинаковой для всех газов. Если умножить обе части уравнения (9.2) на киломоль, то получим уравнение состояния для одного киломоля
pvm=mRT, (9.4)
откуда
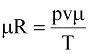 . (9.5)
. (9.5)
Для нормальных физических условий, при которых p=1,013×105 Н/м2, Т=273°К и mv=22,4 м3/кмоль, получим:
 Дж/кмоль×град.
Дж/кмоль×град.
Откуда 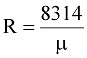 Дж/кг×град.
Дж/кг×град.
Произведение mR называется киломольной газовой постоянной. В связи с тем, что эта величина одинакова для киломоля любого газа, ее называют универсальной газовой постоянной.
9.2.1. Понятие о реальных газах
Реальными называются такие газы, у которых нельзя без значительных погрешностей пренебречь силами сцепления между молекулами, а также объемом самих молекул. К реальным газам, например, относятся водяной пар и пары некоторых других веществ, при состояниях, близких к насыщению.
Реальные газы подчиняются законам идеальных газов только при сравнительно малых давлениях и высоких температурах, так как по мере повышения давления расстояния между молекулами газа уменьшаются, возрастает действие сил межмолекулярного сцепления. В этих условиях уравнение состояния идеальных газов уже не применимо, так как расчеты приведут к большим погрешностям.
Для проведения тепловых расчетов с реальными газами пользуются уравнениями состояния, выведенными для реальных газов с учетом их свойств. Одним из таких, сравнительно простых уравнений, является уравнение Ван-дер-Ваальса
 , (9.6)
, (9.6)
где a и b – коэффициенты, зависящие от природы газа и учитывающие соответственно действие сил сцепления и объем молекул.
9.2.2. Теплоемкость идеальных газов
Для определения количества тепла, которое получает или отдает газ в процессах изменения температуры, необходимо знать его теплоемкость.
Теплоемкостью газа в данном процессе называется отношение количества тепла к соответствующему изменению температуры.
Обычно рассматривают удельные теплоемкости, отнесенные к какой-либо количественной единице вещества.
Так как количество газа принято измерять в килограммах, кубических метрах или киломолях, то различают удельную массовую, объемную и киломольную теплоемкости. Массовая теплоемкость относится к 1 кг газа, обозначается буквой с и измеряется в Дж/кг×град.
Значение теплоемкости данного идеального газа зависит от характера процесса, который протекает в этом газе. Для изучения свойств идеальных газов существенную роль играют теплоемкости процессов при постоянном объеме и давлении.
Рассмотрим два случая подвода тепла к некоторому количеству газа, находящемуся в цилиндре, закрытом поршнем. В первом случае тепло подводится к газу при неизменном положении поршня, т.е. при постоянном объеме газа (V = const). Во втором случае – при неизменном давлении (p = const), но при изменяющемся объеме. Увеличение объема газа во втором случае вызовет перемещение поршня, следовательно, газ совершит некоторую работу поршня.
Рассматривая эти два случая подвода тепла к одному и тому же количеству газа, заключенному в цилиндре, можно сделать вывод, что при одинаковом изменении температуры во втором случае тепла затрачено больше, чем в первом.
Так как здесь газ не только нагревается, но еще и совершает некоторую работу расширения, на что требуется дополнительная затрата тепла. Из этого примера видно, что теплоемкости газа в процессах при постоянном объеме (сv) и при постоянном давлении (cp) неодинаковы, т.е.cp > сv.
Отношение теплоемкостей 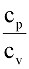 >1, называемое показателем адиабаты k, зависит от атомности газа и в приближенных расчетах принимается постоянным: для одноатомных газов k = 1,67, для двухатомных k = 1,4 и для трехатомных k = 1,29. Для воздуха можно считать k = 1,4.
>1, называемое показателем адиабаты k, зависит от атомности газа и в приближенных расчетах принимается постоянным: для одноатомных газов k = 1,67, для двухатомных k = 1,4 и для трехатомных k = 1,29. Для воздуха можно считать k = 1,4.
Принимать постоянные теплоемкости допустимо только для приближенных расчетов при невысоких температурах. В остальных случаях необходимо учитывать зависимость теплоемкости от температуры.
Теоретические и экспериментальные исследования показали, что теплоемкость газов в значительной степени зависит от температуры, при которой находится данный газ. Эта зависимость тем больше, чем выше температура газа. В области сравнительно невысоких температур (0…100°С) теплоемкость газа изменяется незначительно, поэтому в целях упрощения расчетов пренебрегают изменением теплоемкости и считают её величиной постоянной.
В пневмосистемах возможны различные условия теплообмена между газом и окружающей средой. Например, при малых скоростях течения газа в трубе с хорошим теплообменом процесс вполне можно рассматривать как изотермический.
Если процесс изменения параметров газа протекает быстро и теплообменом с окружающей средой практически можно пренебречь, то такой процесс называется адиабатным и описывается уравнением:
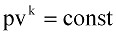
или (9.7)

где k – показатель адиабаты, равный отношению удельных теплоемкостей газа.
Однако в общем случае в зависимости от конкретных условий процессы изменения параметров газа могут протекать с произвольным теплообменом. Такие процессы называются политропическими и характеризуются уравнением

или (9.8)
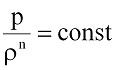
где n – показатель политропы газа, величина которого обычно находится в пределах k ≥ n > 1.
Для некоторых газов при давлении, превышающем 10 МПа, n > k и может достигать значения n = 2 и более.
Для политропических процессов соотношение между давлением р, температурой T, удельным объемом v или плотностью ρ можно выразить как
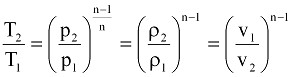 (9.9)
(9.9)
Эта формула будет справедлива и для адиабатического процесса при замене показателя политропы n на показатель адиабаты k.
Приведенные уравнения справедливы лишь для равновесных систем. При движении газа система будет неравновесной. Кроме параметров р, ρ, Т, добавится еще и скорость течения газа υг.
Рассмотрим особенности установившегося течения газа в пневмосистемах, которые необходимо учитывать при истечении газа через отверстие, при заполнении или опорожнении емкостей, при течении по трубам и через местные сопротивления.
Во-первых, принимают за условие, что при установившемся течении массовый расход газа одинаков во всех сечениях вдоль потока:
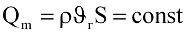 , (9.10)
, (9.10)
где S – площадь сечения потока; υг – скорость течения газа; ρ – плотность газа.
В отличие от течения несжимаемой жидкости, для газа не сохраняется постоянство объемного расхода Q, а расход увеличивается вследствие расширения, вызванного понижением давления вдоль потока, а расширение приводит к изменению температуры (см. уравнение 9.2).
Поэтому уравнение Бернулли для идеального газа отличается от уравнения для идеальной жидкости. Если не учитывать разность нивелирных высот z1 и z2, поскольку плотность газа мала (для воздуха при атмосферном давлении ρ = 1,29 кг/м3), то уравнение Бернулли для политропического процесса можно записать в таком виде
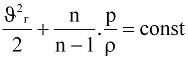 . (9.11)
. (9.11)
В большинстве промышленных пневмосистем происходит адиабатный процесс изменения параметров воздуха или политропический процесс, когда показатель политропы и близок по своему значению к показателю адиабаты k= 1,4.
9.2.3. Приближенные расчеты течения газа в трубопроводах
Как и в гидравлике, расчет течения газа в трубопроводах сводится к определению потерь по длине трубы. По сравнению с течением несжимаемой жидкости течение газа – более сложное явление, связанное, прежде всего с изменением параметров газа вдоль трубопровода и, следовательно, с изменением скорости и режима течения газа.
На практике используют приближенные методы расчета, основанные на допущениях, правомерность которых подтверждена опытным путем.
При достаточно длинном трубопроводе, даже в случае его теплоизоляции, течение газа происходит при постоянной температуре. Если принять, что Т = const, то постоянной также будет и вязкость, а следовательно, и число Рейнольдса Re. С учетом этого потери давления по длине трубопровода могут быть определены по известной формуле гидравлики
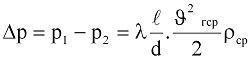 . (9.12)
. (9.12)
где  – коэффициент Дарси (коэффициент гидравлического трения, коэффициент путевых потерь), величина безразмерная;
– коэффициент Дарси (коэффициент гидравлического трения, коэффициент путевых потерь), величина безразмерная; 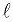 – длина трубопровода;
– длина трубопровода;  – внутренний диаметр трубопровода; ρср – средняя плотность газа; υгср – среднее значение скорости газа.
– внутренний диаметр трубопровода; ρср – средняя плотность газа; υгср – среднее значение скорости газа.
В эту формулу, в отличие от гидравлики, подставляется среднее значение плотности  , здесь ρ1, и ρ2 – соответственно, плотность газа в начале и конце трубы.
, здесь ρ1, и ρ2 – соответственно, плотность газа в начале и конце трубы.
Для круглой трубы среднее значение скорости газа определяется по формуле
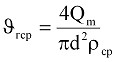 , (9.13)
, (9.13)
где Qm – массовый расход, постоянный вдоль потока газа.
Расчеты и опыты показывают, что течение воздуха в трубопроводах носит обычно турбулентный характер и число Рейнольдса Re находится в пределах от 2300 до 108.
Поэтому величину коэффициента λ, как и в гидравлике, определяют по формуле
(9.14)
где ∆ – абсолютная шероховатость (высота неровностей стенок трубопровода).
Специальные местные сопротивления в пневматических системах, как и в гидросистемах, играют важную роль, особенно при построении систем управления и контроля. Наиболее распространенными специальными местными сопротивлениями являются дроссели, которые в пневмосистемах и гидросистемах выполняют одну и ту же задачу и строятся по одному и тому же принципу.
Считая процесс течения воздуха адиабатическим, массовый расход Qm через пневмодроссель с допустимой погрешностью определяют по формуле
, (9.15)
где µ – коэффициент расхода, который определяется так же, как и для несжимаемой жидкости; Sдр – площадь проходного сечения дросселя; ρср – средняя плотность газа; ; p1 – давление газа перед дросселем; p2 – давление газа за дросселем.
На основании материалов этого раздела можно заключить, что законы статики и законы движения газов и жидкостей для промышленных пневмосистем практически одинаковы. Поэтому назначение, принцип действия, классификация, терминология и условные обозначения основных элементов пневматических и гидравлических систем аналогичны.
Конструктивные же отличия и применение особых пневмоэлементов (кондиционеров и некоторых пневмоаппаратов) обусловлены особенностями газа как рабочей среды.
